09年の冬に、拙ブログにてワンショットパノラマ撮影用のミラーについて整理した記事を転載します。
ちょっと数学用語が出てきて、頭が良さそうに見えますが、計算式は一切使いません。
1.パノラマミラーとは?
2.円、楕円、放物線、双曲線の特徴
3.放物面が凸レンズ代わりになる
4.双曲面で全周ミラーができるわけ
5.双曲面ミラーのピント合わせ
6.意外な楕円面ミラーの考え方
7.楕円面ミラーのピント合わせ
1.パノラマミラーとは?
パノラマミラーとは、カメラのレンズの前に装着することで、水平方向の360度、全方向をワンショットで撮影できるアクセサリーのことです。
ロボットの位置情報検出、監視カメラ、不動産物件のWEB上での紹介などの他、アートのジャンルでも使われます。
撮影例として、このムービーは傑作!
メインとなるのは、凸双曲面ミラーを使うタイプです。例えば、「映蔵」など。
これとは逆に、凹面ミラー使ったEGGもあります。
もともと、これらのミラーを使った時に、いったいピントはどこにあわせればよいの? から始まった疑問なのですが、よくよく考えたら、なぜ双曲面なのか? 凹面ミラーは、どんな曲面なのか? といった重要なことを何一つ知らないことに気付いたわけです。
こりゃ、基礎から勉強しないといけない!
で、アンフィの安藤さんにもご相談申し上げたりしながら、半年ほどいろいろ調べていたのですが、厳密な数式はヌキにして、なんとなく全体像が把握できたような気がします。
まだまだ調べ足りないところはあるのですが、とりあえず整理しておきます。
2.円、楕円、放物線、双曲線の特徴
まず最初は、数学的知識の基礎の基礎、円、楕円、放物線、双曲線とは何か? から。じつは、これらの曲線は全て仲間なのですね。
円錐を平面でカットする時に、その断面はどのような形になるか? を考えると、見事にこれら4つの曲線が出てきます。数学的な意味はわからないけれど、なぜか腑に落ちる感じがします。
(円錐からできる曲線なので、これらを円錐曲線というそうです。)
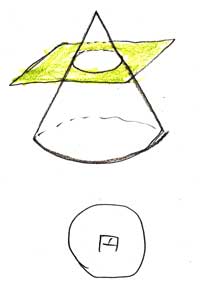
▲円は、円錐を水平にカットした時の接線の形。
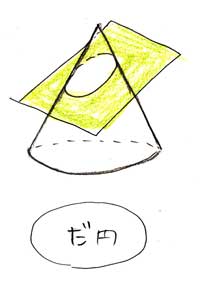
▲楕円は、円錐を斜めの平面でカットするとできます。
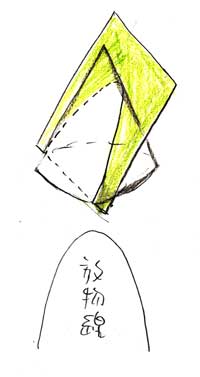
▲円錐の斜めの線に平行な平面でカットすると、放物線になります。
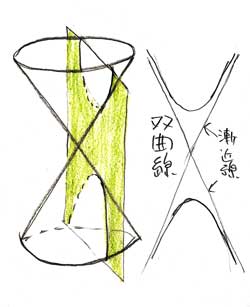
▲円錐を垂直方向にカットすると、双曲線になるのですが、面白いことに、反対側の円錐を想定すると、線は二つ(なので「双」曲線)
こんな知識がなんの役に立つのか? はわかりませんが、面白いです。
3.放物面が凸レンズになる?
引き続き、それぞれの曲線の特徴を整理しておきます。
数学的にはいろいろな特徴があるのでしょうが、ここでは中心や焦点から出た光がどのように反射するか、だけをしっかり理解し
ておきます。理解するというよりも、そういうものだ、と覚えるしかないですけれど。
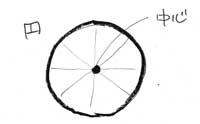
▲円の中心から出た光は、円の内側で反射して、中心に戻ります。
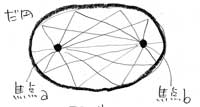
▲楕円は、二つの焦点をもちます。いずれかの焦点から出た光は、楕円の内側で反射して、もう一つの焦点に集まります。これが非常に面白い性質で、凹ミラーを用いたパノラマレンズに使われています。
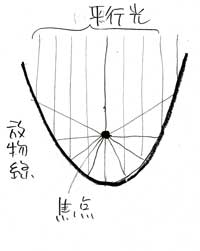
▲放物線をぐるっと回転してできる放物面ミラーは、凸レンズの代わりになることが知られています。反射望遠鏡の原理ですね。
放物線にも焦点があって、ここから出た光は放物線の内側で反射して、平行光線になります。光が逆進していくところを想像すると、凸レンズみたいに光を焦点に集めているのと同じことになります。
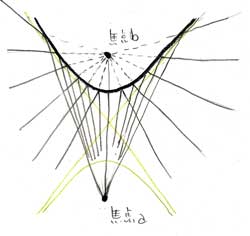
▲双曲線の二つの曲線のそれぞれの内側に焦点があります。ここでは上の曲線だけを考えるのですが、焦点aから出た光は、双曲線の外側で反射して周りに散らばります。
双曲線の面白い特徴は、こうして散らばった光がどこからきたか(?)を探していくと(破線)、焦点bに至るのです。
つまり、焦点aから出た光は、あたかも焦点bから出た光のように見える、ということ。
光を逆に進めていくと、周辺から焦点bに集まってきた光は、焦点aに集まることになります。楕円は、二つの焦点をもちます。いずれかの焦点から出た光は、楕円の内側で反射して、もう一つの焦点に集まります。これが非常に面白い性質で、凹ミラーを用いたパノラマレンズに使われています。
カンのよい人であれば、なんとなくこれが全周パノラマ用ミラーになることがわかるでしょう。
さて、これで準備万端です。 いよいよ次は、双曲線パノラマミラーの性質を調べていきます。
4.双曲面で全周ミラーができるわけ
上の項で、双曲線の焦点と光の進み方が理解できれば、下の図はそれほど違和感なく見られるでしょう。
双曲線をグルッと回転させた双曲面ミラーを使うことで、360度全周を撮影できます。(実は、円錐状のミラーや、球形のミラーでも全周を撮影すること自体は可能です。でもこの話題はちょっと置いておきます。)
カメラのレンズの中心(ノーダルポイント/ノーパララックスポイント)が、双曲線の一つの焦点aの位置と重なるように配置するのが重要なポイントになります。
これにより、「光路長一定の法則」が成立して、鉛直方向の球面収差がなくなります。シャープな像な得るための条件ということです。
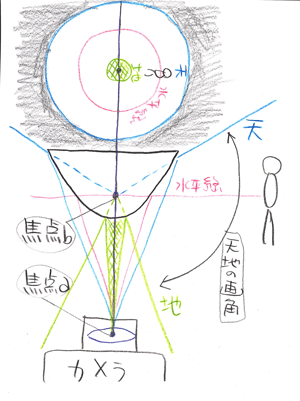
双曲面の焦点bから水平に伸びる平面が、水平線に相当します。ここから、画面端に向けて、実物の上の部分が写ります。逆に画面の中心部に向かって、実物の下の部分が写ります。
天の限界は、双曲面の端の位置(センサーサイズとの関係がある)で決まります。
地の限界は、カメラなどが写る範囲となります。
図の上にはだいたいこんなイメージで写ることを示しましたが、正確な撮影イメージを描くには、ピントがどこに在る(合う)か? を調べなければなりません。
ただ、単純に、カメラのピントは、双曲線の焦点b付近に合わせる必要があることは確かでしょう。つまり、このミラーを使った撮影には、マクロレンズが必要、ということです。
さらにこの図からわかるのは、センサーサイズをできるだけ有効に使う(画面の円の直径がセンサーサイズの短辺に合う)ためには、カメラのレンズの中心と双曲面ミラーの焦点を合わせつつ、ズーム(画角)を最適化することが必要です。
どうなのでしょう? 簡単にできるのでしょうか?
5.双曲面ミラーのピント合わせ
双曲面ミラーのピント合わせはどうするか? ここまでで、マクロ撮影になることまでは、わかっています。
下の図では、水平線の高さ(赤線)の被写体を考えています。
青線が無限遠にある被写体からの光で、双曲面で反射して広がります。広がった光を反対側に追いかけていくと、双曲面の上の方で焦点を結すぶことがわかります。水平線の高さの無限遠の被写体ですから、焦点は赤線上にあります。
緑の線は近い被写体からの光です。同様に双曲面で反射し広がりますが、無限遠円の光よりも広がります。このため、無限遠の焦点位置よりも下に焦点を結びます。
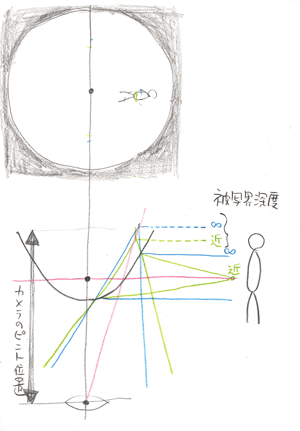
この作図からわかることをいくつか。
1)双曲面でできる被写体の像(虚像)は、双曲面の焦点位置よりも奥にできる。カメラのレンズのピントは、ここに合わせる。
前回描いた像のサイズよりも、一回り大きな像になることもわかる。
2)青線と緑線の焦点の位置が縦(カメラのレンズの光軸方向)にずれる・・これが被写界深度になる。無限遠よりもカメラよりの方に近点ができるので、無限遠のピント位置よりも奥にピントを合わせる必要はない。<
・・・・・双曲面の調査はこれでひとまず終わります。
(実をいうと、像面が本当に平面になるかどうか、もわかっていません。作図でやるには限界がありそう。数学的に計算するには、勉強のし直しが必要です。)
次は凹面を使ったパノラマミラー(EGG)を調べます。
6.意外な楕円面ミラーの考え方
凹ミラーを使ったパノラマシステム「EGG」について。なんとなく双曲面の逆関数(?)みたいな線でできるんじゃないの。とか思っていたのですが・・。どうも怪しい。
円錐曲線を調べていたら閃きましたよ。
そう、楕円なんですよ。(多分)
考えてみれば、「EGG(卵)」ではござんせんか!
下図に描いたよう、楕円の片方の焦点aを中心に偏心させた楕円面の内側を使っているようです。
もう一つの焦点bは、楕円を回転させる時に一緒に回転するため、焦点というよりも、焦円(?)になることにも注意しておきます。
焦点aをカメラのレンズ中心に合わせると、光路長一定の法則が成立しますので、球面収差を無くせます。
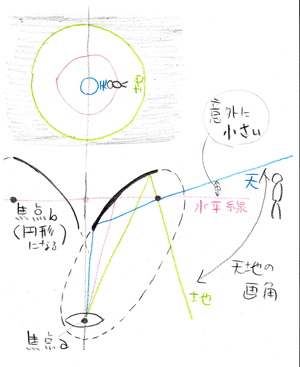
この作図からわかること。
1)双曲面ミラーとは違い、像の天地が逆になる。上の円形の図の人の頭が中心側を向いている。
・・画像を長方形に展開する時、天の方がデータ補完が多くなる。逆に地の方はデータが目一杯あるのでOK。
2)被写体の上の部分(天)を撮るのに限界がある。
楕円ミラーの下の部分がカメラのレンズ中心からはみ出すことができないため。
下(地)は、カメラ本体などに邪魔されない限りok。(双曲線ミラーと同じ)
・・・・実際にEGGの作例を見ると、上(天)を撮るのにかなり限界があることがわかります。画像の水平線は意外なほど上にあり、人の目線よりも少し高い位置にカメラをセットしているのではないかと思えるほどです。この限界は、実際の撮影では、結構厳しい条件になるように思います。
「被写体を選ぶ」ということですが。
さて、次は、楕円ミラーのピント合わせを調べます。
7.楕円面ミラーでのピント合わせ
楕円ミラーのピント位置を、双曲線ミラーと同じように作図してみました。
要領は同じですので、難しくはないはずです。
被写界深度や像のズレも双曲面ミラーと同じ要領。
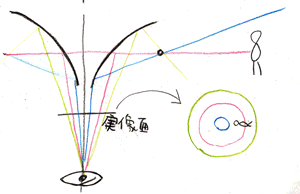
大きな違いは、楕円ミラーでは「実像」ができること。
そして、ミラーとカメラのレンズの間にできることです。
★★蛇足
作図はしませんが、円錐ミラーを想定してみると、これは双曲面ミラーや楕円面ミラーのように焦点は結びません。鏡に向かって撮っているのと同じことです。
双曲面ミラーは、ミラーの奥に虚像を作ります。これは凹レンズと同じ。
楕円面ミラーは、ミラーの手前に実像を作ります。これは凸レンズと同じです。
双曲面~平面~楕円面が、ひとつながりになりそうです。
では、球面は? あれれ? いずれ考えてみましょう。
・・・中途半端に、とりありずここまで。
